円の性質 弦と弧 円周と2 点で交わる直線を割線という。 このときの交点を 2 点 a, b とするとき、円周によって、割線から切り取られる線分 ab のことを弦といい、弦 ab と呼ぶ。特に円の中心を通る割線を中心線という。中心線は円の対称軸であり、円の面積を 2 等分する。・おうぎ形の折り返し問題正三角形が表れる。 ・図形を回転させる問題同じ面積の部分がある。 ・円を転がす問題直角マークを書く。 ・太陽光の問題太陽光の最後から真横に補助線。 ・電灯光の問題1つの図の中に,相似三角形あり。 図形のまわりの長さが同じ場合、もっとも面積が大きくなるのは"円" なのです! まとめ 周りの長さが同じ図形で、一番面積が大きいのは"円" 正方形もそこそこ大きい;
求積問題 正方形と扇形
円 正方形 面積 同じ
円 正方形 面積 同じ-入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 女子校 直角三角形 4年生 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 二等辺三角形 直角二等辺三角形 立体の切断 ファイ内側の正三角形,内側の正 方形を回して下の図のように する。 3cm 6cm A B C E D A B 30° 70° 140° 1 2 もう,円はいらないので, 取ってしまう。 外側の正三角形の面積を1とすると, 内側の正三角形は,-になる。 ☆ ☆ ☆ ☆ 4 1
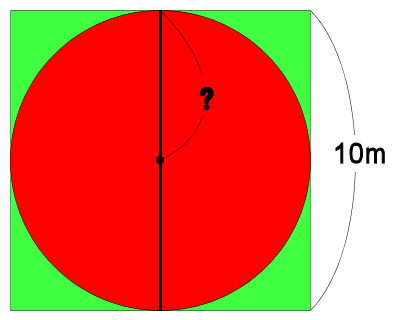



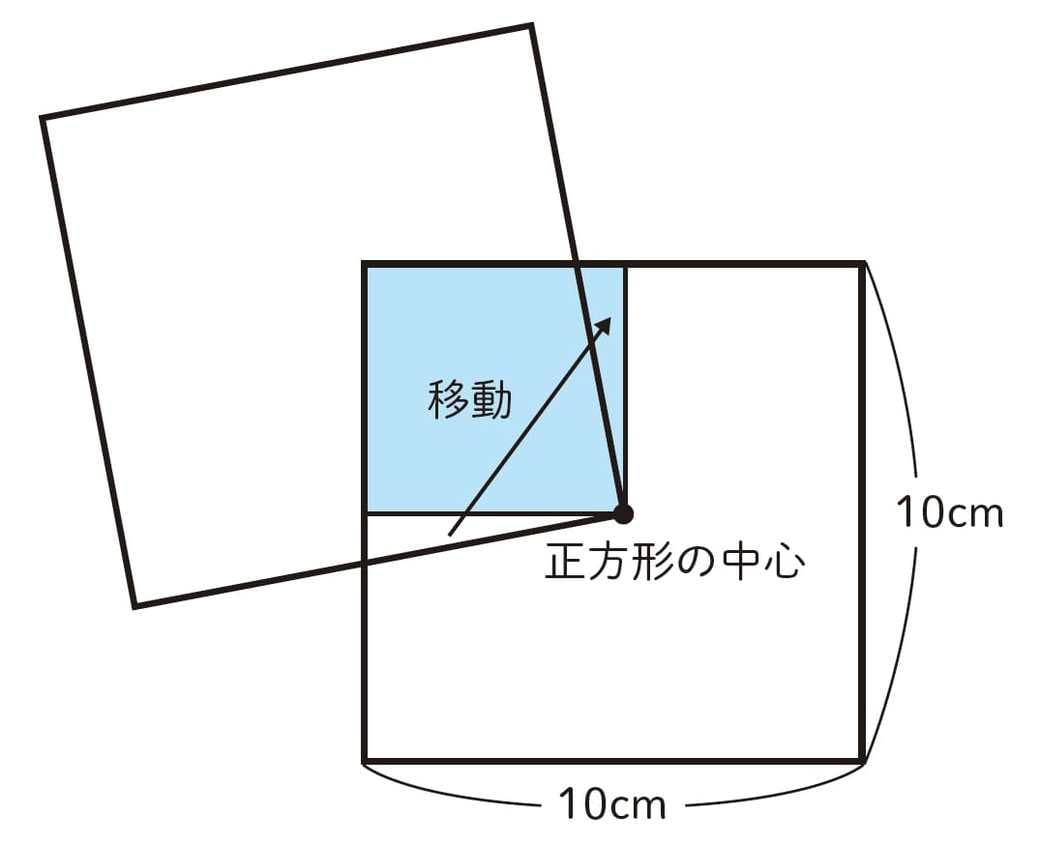
円の面積 正方形の中に円
平面充填(へいめんじゅうてん)とは、平面内を有限種類の平面図形(タイル)で隙間なく敷き詰める操作である。 敷き詰めたタイルからなる平面全体を平面充填形という。 平面敷き詰め、タイル貼り、タイリング (tiling) 、テセレーション (tessellation) ともいう。円の面積半径×半径×314 高さが80mの三角形の面積を引いたものと同じ おうぎ形DBCの半径をrにすると、正方形EFCGの 面積はr×r÷2平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さ
円積問題えんせきもんだい 与えられた 円 と同じ 面積 をもつ 正方形 を定木とコンパスで 作図 できるか、という問題をいう。 古代 ギリシアの三大 作図不能問題 のうちの一つである。 半径1の円の面積はπであるから、この問題は の長さの線分を定木とコンパスで作図できるか、という問題と同じである。 有理数を係数とする多項式(係数が全部ゼロである場合正三角形の面積は 1 2 2 p 3 = p 3 だから それと同じ面積の正方形の一辺は4 p 3 したがって前図で四角形WXYZ は正方形 辺上にある4 つの点P, Q, R, S のうち3 つをテープ で留めるなどしてつなげておくと、つながったまま 正方形に変形できる円に内接する正多角形 後から星形をカッターで切り抜いた。 大きさは色々でも、形が揃う為。 円を近似するのに何角形くらいで十分か確認するために使用しました。 ありがとうございます! じゃがいもの面取りで効率が良いのは7面というお話があり、数値を出すために使いました。 じゃがいもを円柱と見立てた場合の廃棄率は、6面1730%、7面1290%、8面997
弧ac(c)は半径10の円の12分の1の面積の扇なので 100π×12分の1. 残ったa(c)(d)とacdの面積は足すと正方形abcdの面積と同値になるから50. 図形全体の面積から正方形abcdの面積を引くと、 スポンサーリンク 子供の勉強を教えていると、算数なんかは特にどう説明したらいいのか 迷うことが多いです。 これもそういう問題の一つかもしれません。 問題 周りの長さがどちらも同じである、長方形と正方形の面積は同じでしょうか。 違うでしょうか。理由は? 答えは、後 ルール1 円の中の正方形の面積は、その円の半径を1辺とする正方形の面積の2倍 を 少し変えるとルール2になります。




説明お願いします Clear




Twitterで拾った問題 半円に接する2つの正方形 オンライン講師ブログ
円と同じ面積の正方形の作図 数学と社会の架け橋<数学月間> 円と同じ面積の正方形の作図 (Thu) ギリシャの幾何学者達が研究した不可能作図は,以下のようなものです. (1)与えられた正立方体の2倍の体積の正立方体を作れ (2)与えられた円と同じ面積の正方形を作れ (3)任意に与えられた角を3等分せよ 定規とコンパスだけを有限回使って作図<円とおうぎ形 面積その5> (図1)は,1辺が8cmの正方形ADの中に円をかぎその円に正方形EFGHをかいたものです。ただし,円周率は314とします。 (1) 正方形EFGHの面積は何cm2ですか。 (2) かげをつけた部分の面積は何cm2ですか。 図2)は,半径6cmの半円です。歴史 与えられた円に対し、それに近い面積の正方形を近似的に求める方法は バビロニアの数学者 にも既に知られていた。 紀元前1800年 頃のエジプトの リンド数学パピルス には、直径が d {\displaystyle d} の円の面積は 8 2 9 2 d 2 {\displaystyle {\frac {8^ {2}} {9^ {2}}}d^ {2}} 、即ち 64 81 d 2 {\displaystyle {\frac {64} {81}}d^ {2}} だと記載されている 。
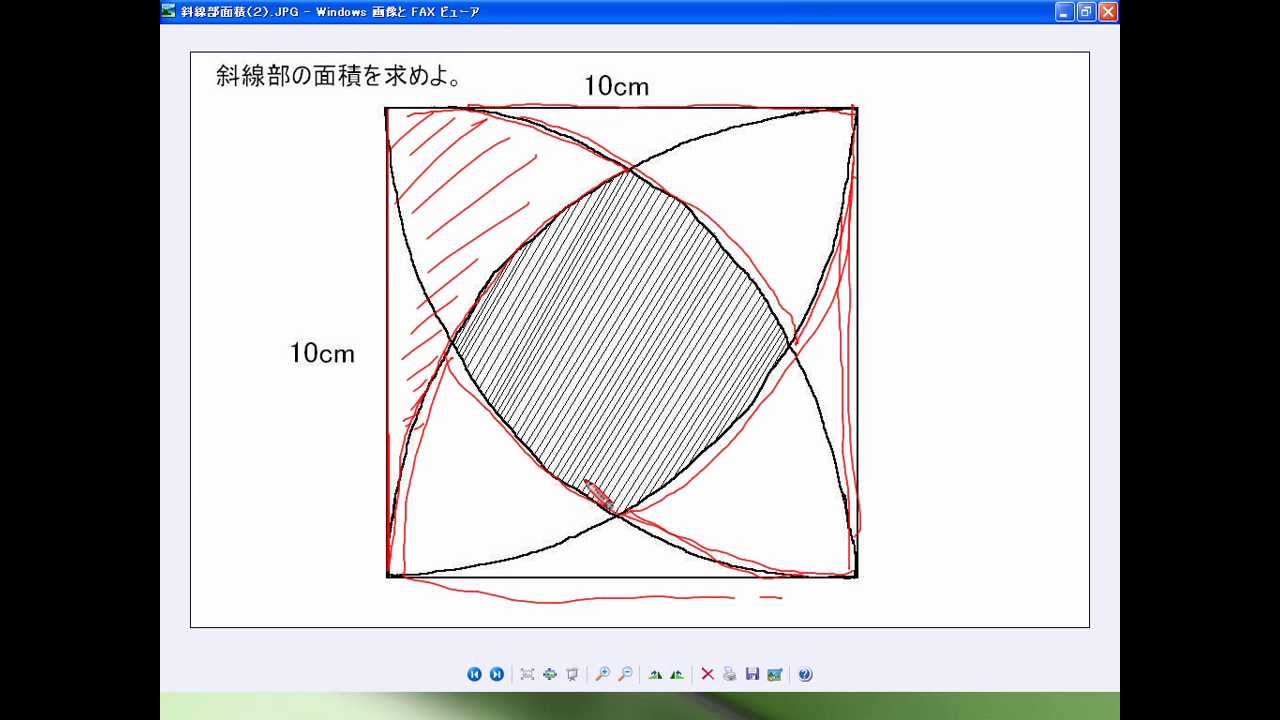



斜線部の面積 4 1辺10cmの正方形の場合 Youtube




円の面積 正方形の中に円
円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ円の面積 円の面積は,半径×半径×314で求められます。 この求積公式の指導にあたっては,公式の理解はもとより,そこに至る過程を大切に指導することが重要です。 まず,半径10cmの円の面積が半径 (10cm)を1辺とする正方形の面積のおよそ何倍になるか円と円の間の空間 同じ大きさの円を図 1 のように並べる。 図 1 3個の円の中心を結んでできる正三角形を隙間なく並べると図 1 を再現できる。 したがって,この正三角形の面積とその内部にある扇形の面積との比は,全体のその比に等しい。 図 2




朝日新聞デジタル 円の面積 正方形を使って考えよう 山上浩二郎の大学取れたて便 大学 教育



第二十回 黄金律と円積法 By 岡田恒良 自他一如 医の現場から見えること Tao Lab Magazine
314×36= 314×49= 314×64=096 314×81= 正方形や円などの面積を速く正確に計算するために、同じ数をかけた積(二乗・自乗)の計算方法をマスターしましょう。 (参考) → 二乗の速算法 平面図形の面積の基本問題 問題1任意の正方形 d の辺のどれとでもよいから入れ替えるならば、面積は同じで、しかも合同にはならない。 共円四辺形の面積は、辺の長さが隣り合う順に a, b, c, ただし K はこの共円四辺形の面積で次は、円と同じ面積を持つ正方形はどうすればできるだろうか。 円積問題とは、 (参考)ギリシア数学の三大難問とは、 ・ 倍積問題 (与えられた立方体とちょうど2倍の体積をもつ立方体を作れ。) ・ 角の三等分 (与えられた角を三等分せよ。




関数の基礎 使い方 今日からpython



円の面積問題のようですが 筑波大学附属中学 2008年 パズル算数クイズ
Φ600の内接する正八角形の1辺の長さを求めたかった ご意見・ご感想 円の半径r=300でのn=8の多角形の1辺の長さaはではなくて?ではないでしょうか。 keisanより r=300の時、辺の長さがとなるのは、 円に外接する正多角形と考えられます。円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さ同じ面積の三角形から、同じ三角形( obc)を取り除いて できあがった図形は( aboと dco) もちろん面積が等しくなるはずだよね! だからです。 台形の中から等しい三角形を見つける問題では



面積 算数星人のweb問題集 中学受験算数の問題に挑戦



円の相似を利用した面積の計算 中学受験プロ講師ブログ
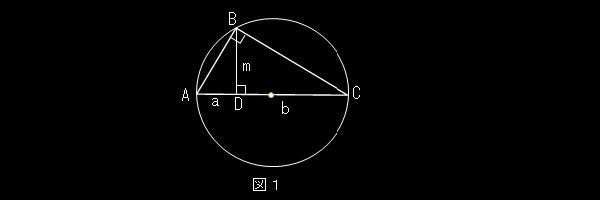
面積は で、辺長 s の正三角形の面積の 倍、直径 s の円の面積の 倍である。ブラシュケ・ルベーグの定理より、これは幅が同じ定幅図形の中では最小である。AD=a ,DB=b AB(=a+b)を直径とする円とDからの 垂線との交点をCとする。 このとき、 ADC∽ CDBから DC=√(ab) とわかる。 これは前の「面積の二等分」の 私の解答にも利用しました。 長方形を同じ面積の正方形に変える作図は つぎのようなものではなかったんですか?



Www Chuo Tky Ed Jp Harumi Jh Resources Content 3561 0421 Pdf
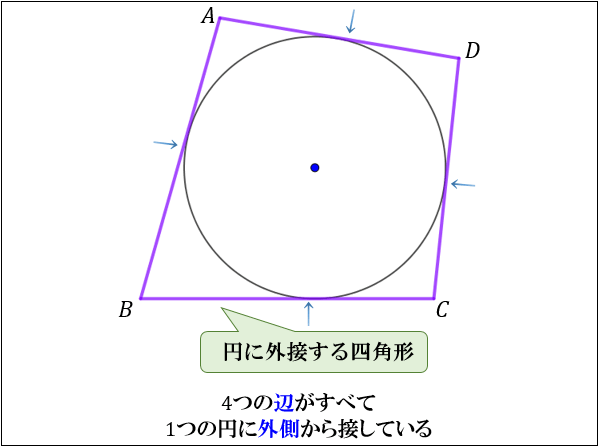



円に外接する四角形の性質まとめ 向かい合った辺の合計が等しくなる理由 アタリマエ



6年算数 円の面積 2 わかる教え方



円と扇形 中学受験ー算数解き方ポータル




ある正方形の2倍の面積のものを書きましょう この問題の解き方を教え 数学 教えて Goo




z会 Asteria う 数学 面積が等しい シリーズ 今回のテーマは正多角形 同じ円 に内接する正五角形 正六角形 正十角形 それぞれの辺を1辺とする正方形を考えると 小さい2つの正方形の面積の和は 大きい正方形の面積と等しくなります




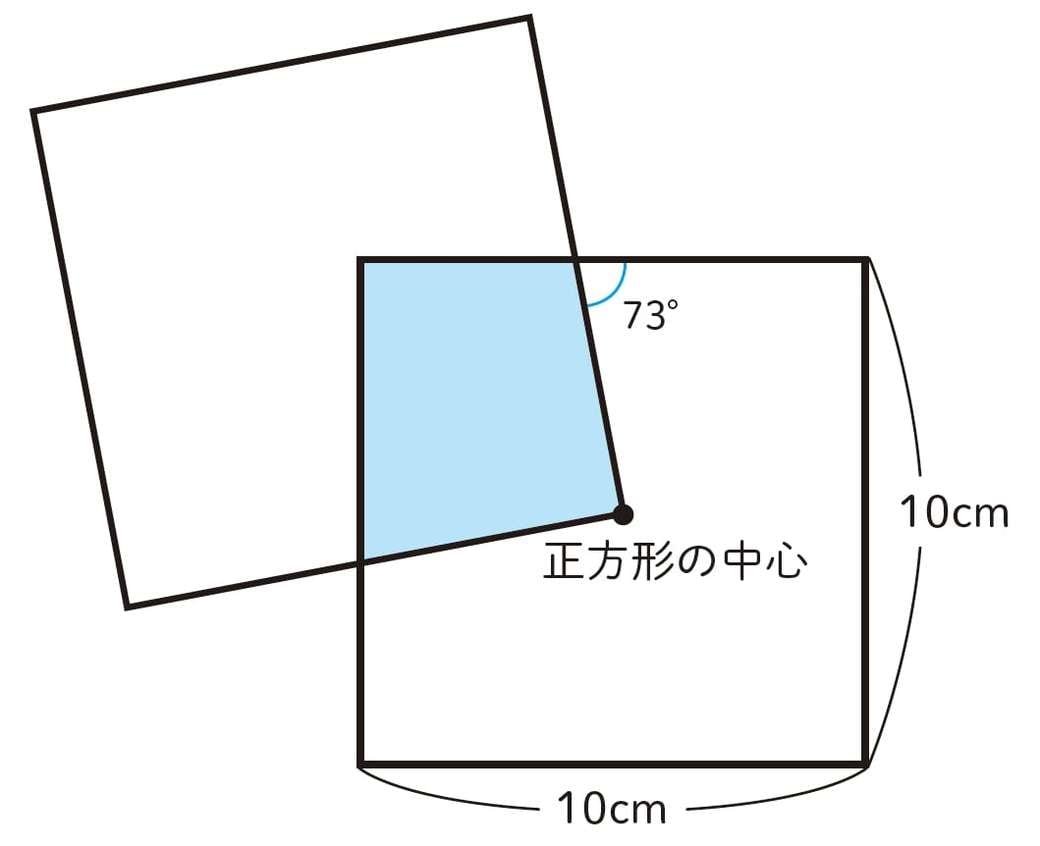
正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく
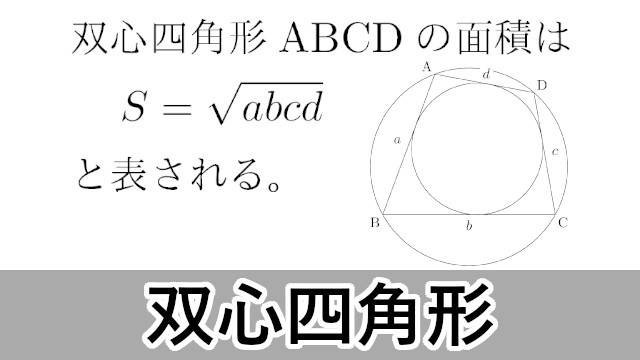



双心四角形の面積 外接円と内接円の両方をもつ四角形 大学入試数学の考え方と解法



小学算数で斜線部の面積を出してください 正方形の面積は Yahoo 知恵袋



円と等しい面積の正方形の作図について Togetter




超頻出 正方形の中に正方形の面積問題 恋する中高一貫校 適性検査 徹底攻略




6 Lihat Cara Penyelesaian Di Qanda




円と同じ面積の正方形の作図 数学と社会の架け橋 数学月間



アタマを柔らかくする 脳トレ数学クイズ3選 リーダーシップ 教養 資格 スキル 東洋経済オンライン 社会をよくする経済ニュース
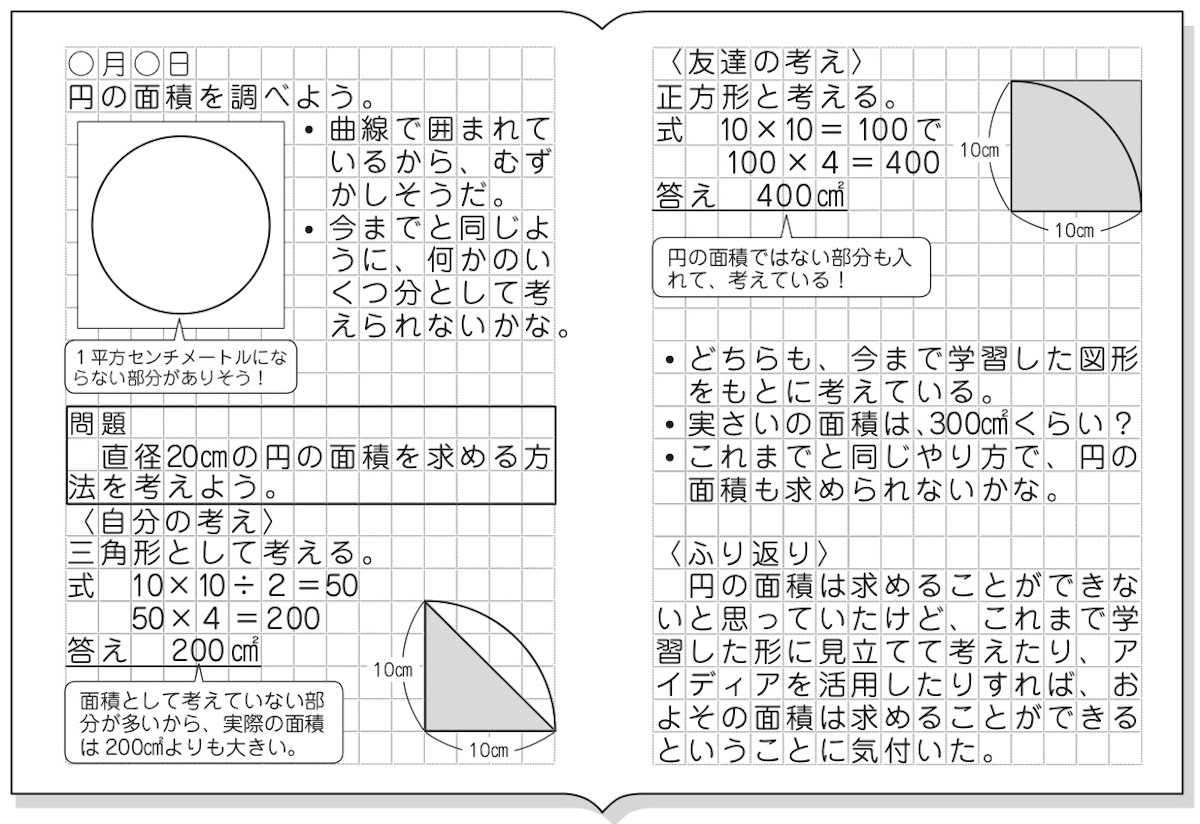



小6算数 円の面積 指導アイデア みんなの教育技術




今日は 円を使って正多角形をかく自主学習をしてみましょう 正多角形は 多角形の中で次のような条件を満たすものです すべての辺が同じ長さ すべての角が 同じ長さ 正三角形や正方形も 正多角形 学習ノート 中学数学




球の表面積と同じ面積をもつ正方形の作図方法 花鳥風月あめあられ




長方形 正方形の面積 練習 Youtube




正方形と円で囲まれた図形の面積 おわり Takapの数学日記




重なった正方形の面積 スクールプレゼンター教材共有サイト スクプレ道場
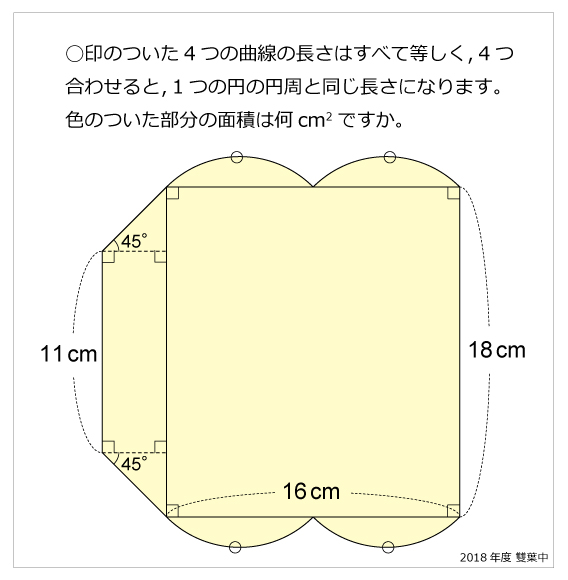



面積 算数星人のweb問題集 中学受験算数の問題に挑戦




超頻出 正方形の中に正方形の面積問題 恋する中高一貫校 適性検査 徹底攻略
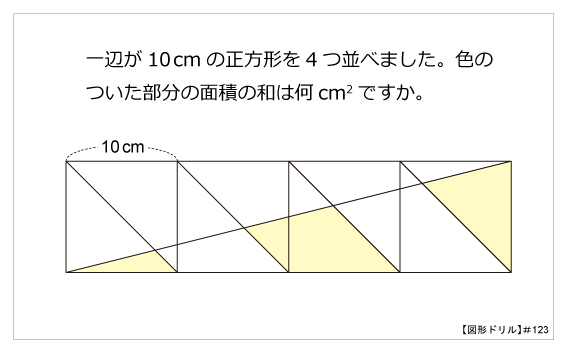



図形ドリル 第123問 正方形と面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦




数学の世界をのぞいてみよう 第41回 与えられた長方形と同じ面積の正方形を描いてみよう Segブログ 科学的教育グループseg



球の表面積と同じ面積をもつ正方形の作図方法 花鳥風月あめあられ




ユーザーインタフェースにおける視覚効果 Frasco




ユーザーインタフェースにおける視覚効果 Frasco
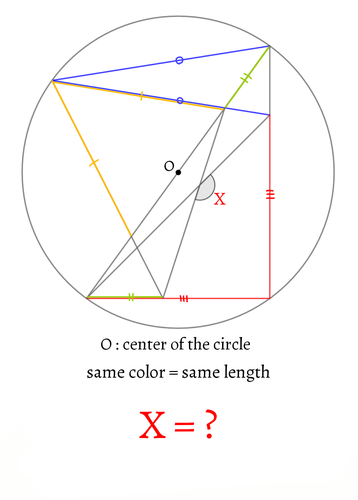



求面積問題 ポロロッカ
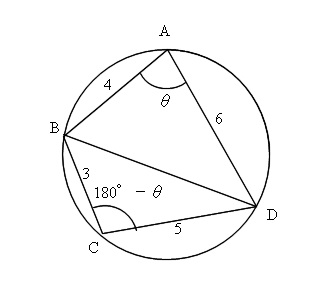



円に内接する四角形の面積の求め方と定理の使い方




Mondai55




浅野 円の面積を比べる ジーニアス 中学受験専門塾



内接する円の問題 中学受験 田中貴 Com




6年算数 円の面積 2 わかる教え方
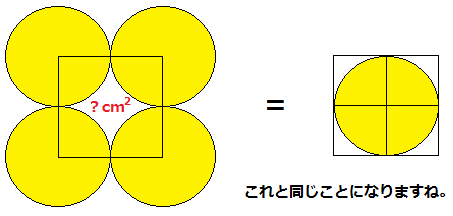



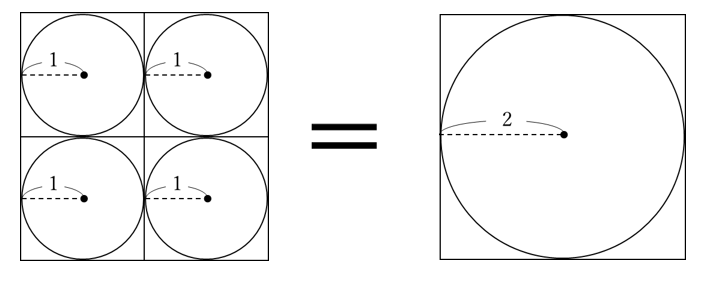
4つの円のすき間の解答と解説 多目的ルーム 楽天ブログ
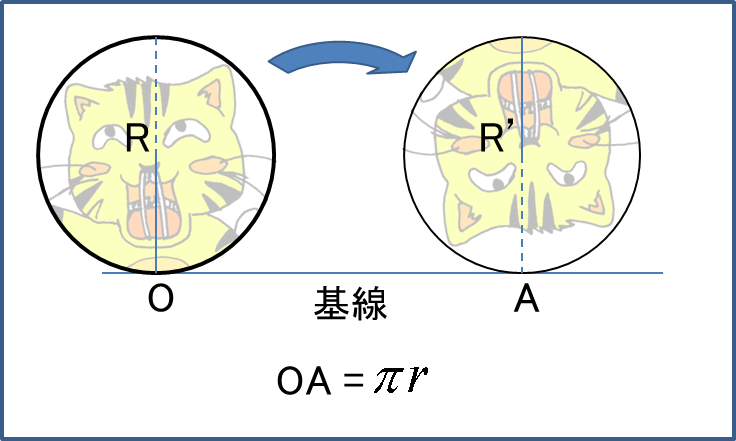



円と等しい面積の正方形の作図について Togetter
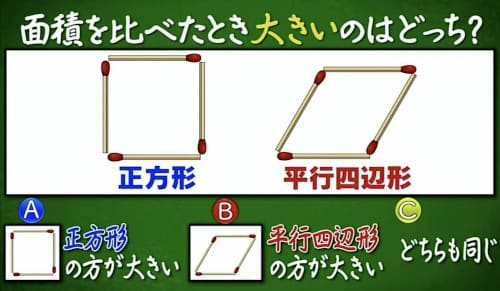



正方形と平行四辺形の面積の話 クイズ あなたは小学5年生より賢いの 12 25 何ゴト
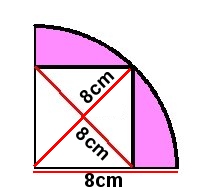



扇形と正方形




円と等しい面積の正方形の作図について Togetter




Nams出版プロジェクト 正方形と同じ面積の正三角形の作図
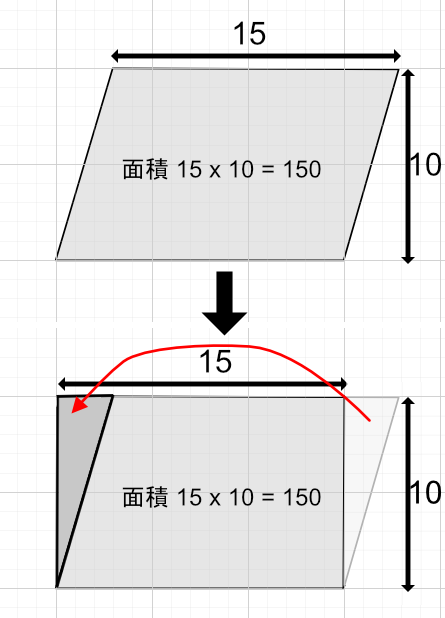



中級 符号 分数 小数 面積 円周率 Shade3d チュートリアル



円積問題



アタマを柔らかくする 脳トレ数学クイズ3選 リーダーシップ 教養 資格 スキル 東洋経済オンライン 社会をよくする経済ニュース



円積率 雑学のソムリエ




円と等しい面積の正方形の作図について Togetter



図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト




公式なんて覚えない ひし形の面積は直感的に考えよう



円と等しい面積の正方形の作図について Togetter



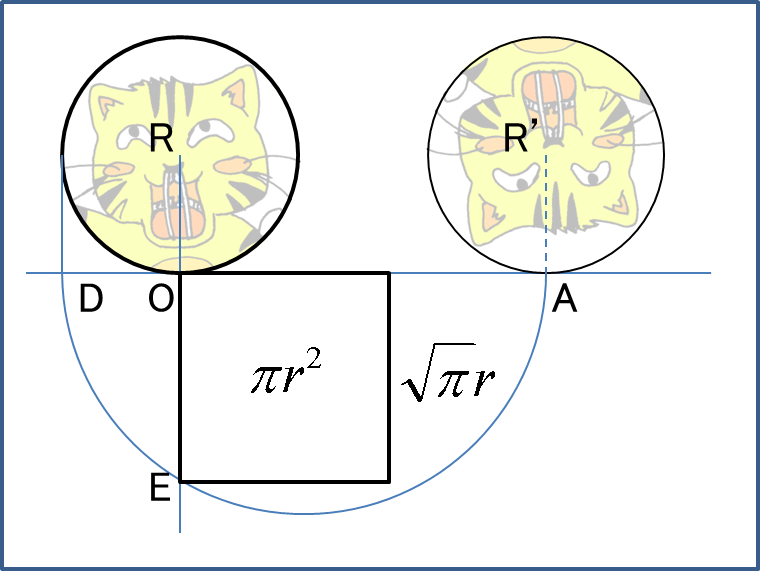
正方形と円の面積が同じとき 正方形の一辺の長さは円の半径の何倍かについておしえ Yahoo 知恵袋




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



正方形と同じ面積を持つ円の共通部分の面積 日曜研究室



求積問題 正方形と扇形



正方形と円の面積が同じとき 正方形の一辺の長さは円の半径の何倍かについておしえ Yahoo 知恵袋




二次方程式が 図形 で解ける X 発明前の数学に挑戦しよう 横山 明日希 ブルーバックス 講談社 4 4



図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト



円の相似を利用した面積の計算 中学受験プロ講師ブログ
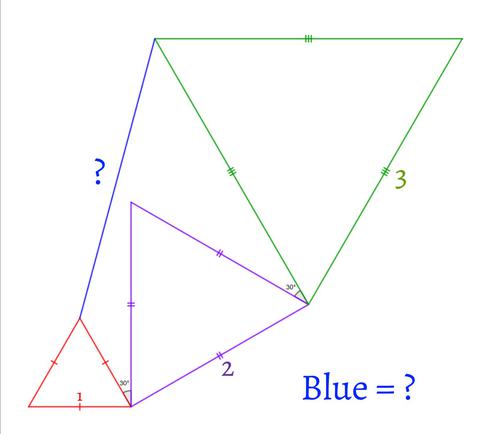



求面積問題 ポロロッカ
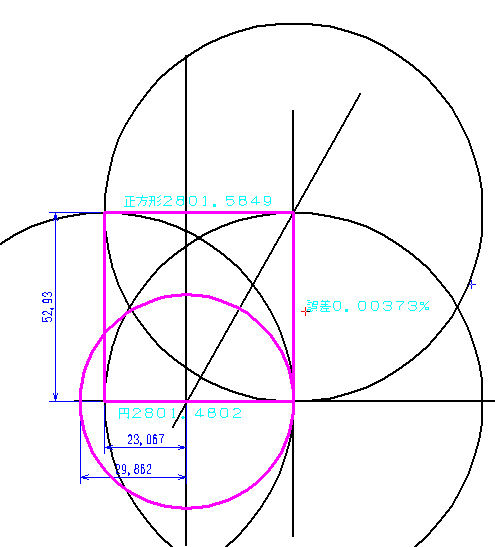



小学校で学べる円積問題 60 直角三角定規を使った線分比例定数 Pの描き方 発想力教育研究所 素数誕生のメカニズム




円の面積 算数用語集




円積問題 Wikipedia



1



求面積問題 ポロロッカ




中学受験算数 平面図形編 Flashcards Quizlet



円とおうぎ形の面積 唇の形 カテキョウブログ
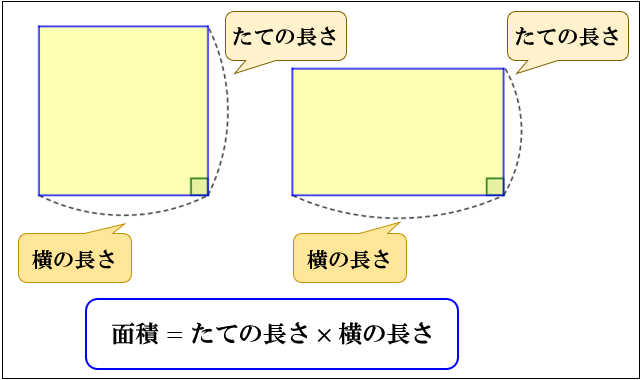



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
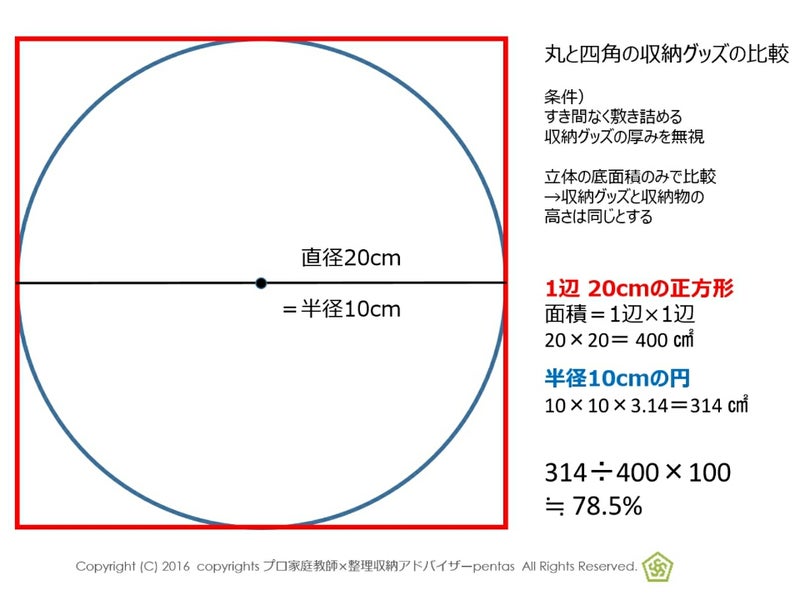



収納量の比較 数学の先生が 四角と丸の収納力を計算したら 中学受験から大学受験の塾プリント整理専門 プロ家庭教師 整理収納アドバイザー中島亜季 大阪京都奈良
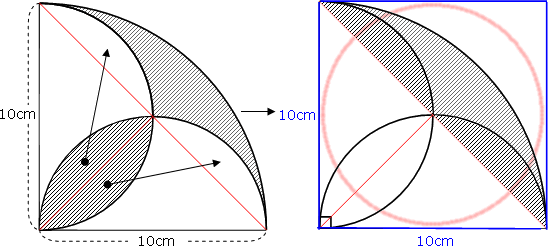



面積の求め方 算数の教え上手 学びの場 Com




中学受験の円に関する問題 角度 長さ 面積の基本問題まとめ 算数数学苦手克服 家庭教師のマスコンサルティング



長方形 正方形
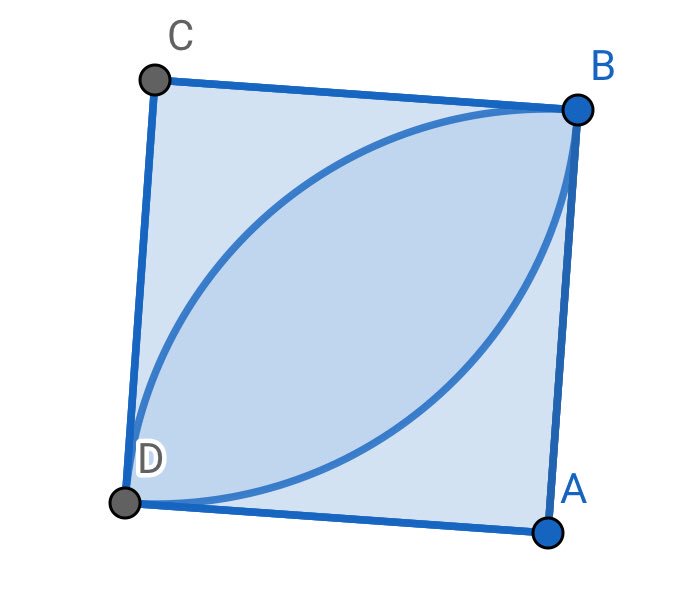



すど Auf Twitter これのことです 本当の面積はab 1 とすると P 2 1 なんだけど 中学受験では円周率は 3 14 なので この面積は0 57 正方形の面積 なんですね だから 0 57 が円周率と同じように暗記の対象になっていたりする 不思議な世界でしょう




Newtonライト さんすうパズル 図形編 ニュートンプレス




標準 おうぎ形と正方形の面積 なかけんの数学ノート




Mml第3回 長方形と同じ面積の正方形を作る リメイク版 Youtube



半径1の円と同じ面積の正方形は一辺の長さが何になりますか また 二つの図形 Yahoo 知恵袋



Pronity 57 球の直径 円周 面積 体積に合わせた 正四面体 正三角形と立方体 正方形の比例



Http Www Qingdaojs Org Rinjikyuukoutyuunoosirase Kadai Kadai7 Suugaku7 Pdf



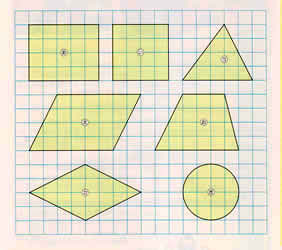
面積の求め方 算数の教え上手 学びの場 Com



円の面積 面白ゼミナール
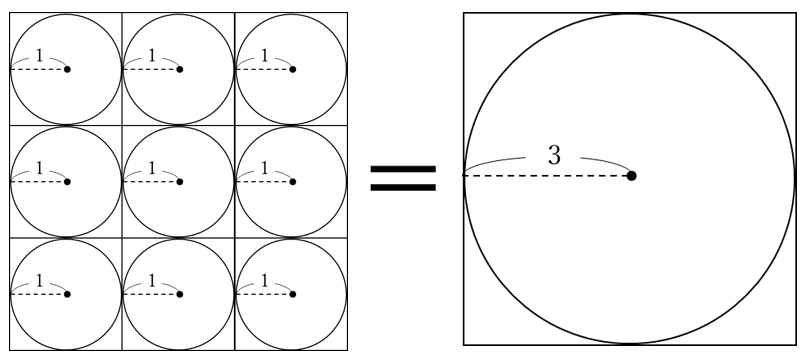



円の相似を利用した面積の計算 中学受験プロ講師ブログ



1



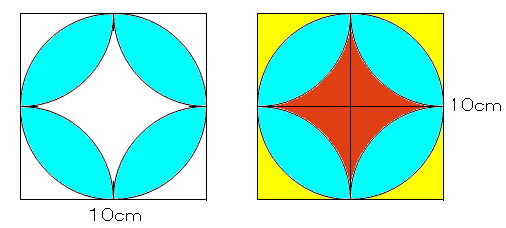
円の面積 1 5




モモのちょっと気になる話 Ssブログ



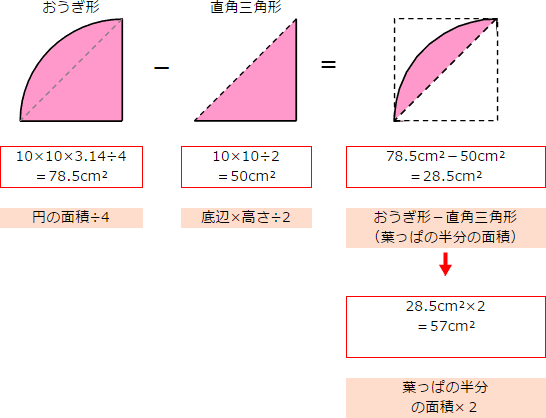
算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素




高校数学 円に内接する四角形の計量 基本と裏技のまとめ トレミーの定理 ブラーマグプタの公式他 受験の月
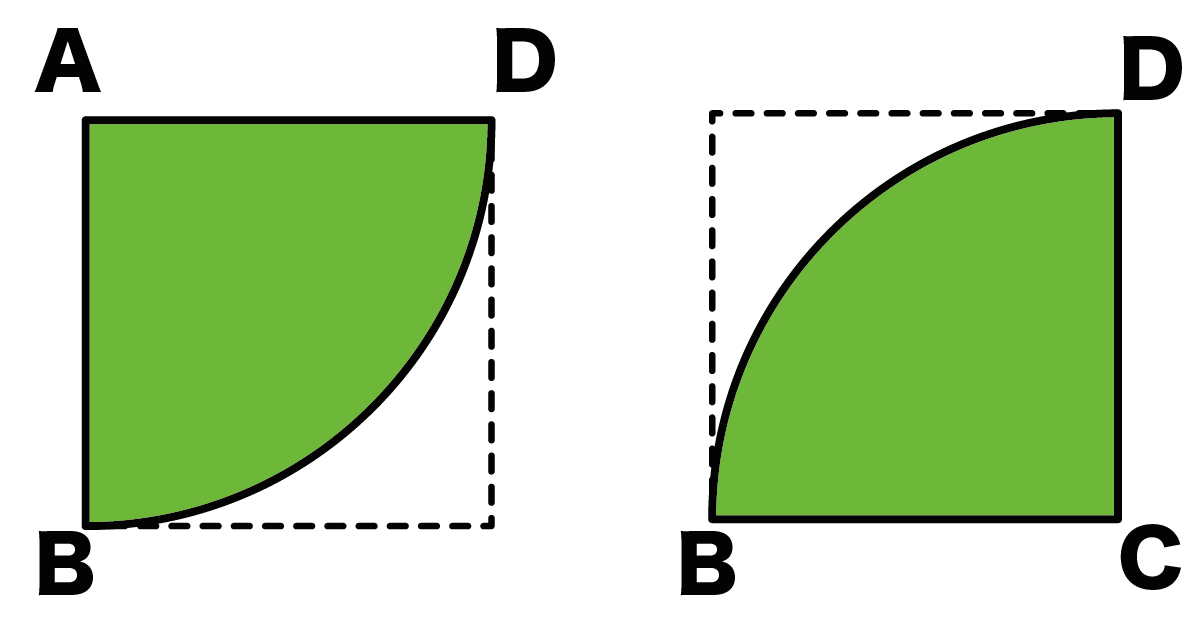



正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




この図で正方形の面積が13平方センチのときの円の面積を求めなさい 小学校 教えて Goo




数学に長けておられるとお見受けしたので さんすうの質問です 単位は省略 円周率は切捨 計算が違っていたらすみま Peing 質問箱




平面図形の苦手を解消 三角形の面積比 基本編



正方形の面積



円積問題 Wikipedia




円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun



正方形と円の面積が同じとき 正方形の一辺の長さは円の半径の何倍かについておしえ Yahoo 知恵袋


